Kepler
Johannes Kepler (1571-1630), a Protestant, was born in Weil, Germany and later graduated from the University of Tübingen where he learned about the Copernican theory. He taught at the Lutheran school in Graz, Austria for a while, but later left rather than convert to Roman Catholicism. He then accepted a position in Prague, in what is now the Czech Republic, as the assistant to Tycho Brahe. Tycho Brahe (1546-1601) was the greatest pre-telescopic astronomical observer. He had an observatory on the island of Hveen, about 32 km northeast of Copenhagen, which was equipped with the most accurate observing equipment at that time. The observing equipment at that time were ones used by the naked eye, such as astrolabes and quadrants. Brahe had help from Frederick II, the king of Prussia, to build his observatory and made the most accurate observations before telescopes.
After Brahe died, Kepler, who was a believer in the Copernican model, tried to find an orbit for the planet Mars that fit Brahe’s observations. Until that time astronomers thought that the orbits of the planets were circles or combinations of circles, but Kepler could not find a system of circles that fit the observations. Kepler then tried an ellipse for his calculations and it worked. He formulated three laws of planetary motion based on Brahe’s work. These laws are listed below.
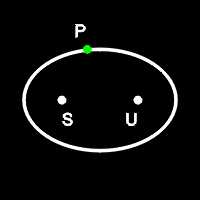
Law 1: The orbit of each planet is an ellipse with the sun at one focus of the ellipse and with the other focus at an unoccupied point in space. The first and second laws were published in Astronomia Nova. See Ellipses.
 |
| Figure 1: An illustration of Kepler's first law. The planet (P) orbits the sun (S) in an elliptical orbit with one focus on the sun and the other focus on an unoccupied point in space (U). |
Law 2: Each planet revolves around the sun so that a line connecting the planet to the sun (the radius vector) sweeps over equal areas in equal times. This is illustrated below.
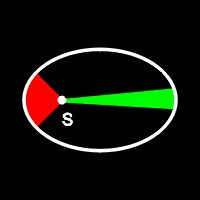 |
| Figure 2: An illustration of Kepler's second law. The a line from the sun (S) to the planet sweeps out equal areas in equal times so the planet moves faster the closer it is to the sun. |
Law 3: The square of the sidereal period of any planet is proportional to the cube of its mean distance from the sun. This law was published in Harmonices Mundi and is sometimes called the harmonic law. It allowed astronomers to calculate the relative distances from the sun of any planet from measurments of its orbital period.
The mathematical form of Kepler’s third law follows.
P is the planet’s sidereal period of revolution.
A is the mean distance of the planet from the sun.
K is a constant whose value depends on the units used for p and a.
![]()
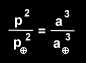
Kepler did not know the value for K but could eliminate it by assuming that it was the same for all planets and writing a ratio for two planets, usually one of them was earth. This equation follows.
The subscript ![]() means earth
means earth
If we express a planet’s sidereal period in sidereal earth years and its mean distance to the sun in astronomical units (AU - the mean distance from the earth to the sun) then, for the Earth, a = 1 and p = 1. Thus, Kepler’s third law becomes the equation below. Kepler did not know the value of AU but it was later found to be 149,597,871 kilometers.
![]()
Kepler’s third law was later refined by Newton to make it more accurate. Newton discovered that K is not quite a constant because the mass of the planets, although small compared to the solar mass, is not quite zero.
If you do not see frames, click here to go to the frames page.
If you do not want to use frames, click here to go to the non-frames home page
and sitemap.