Cones and Conic Sections

The Cone:

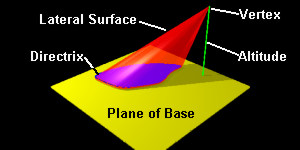
A cone is a solid 3D mathematical shape which lies on a plane and is bounded by a closed curve on the plane (usually a circle) called the directrix (the edge of the blue shape in the figures below). The lateral surface (side) of the cone consists of all of the line segments that intersect the directrix and a point not on the plane called the vertex. The altitude (height) of a cone is the line segment which is perpendicular to the plane of the base and intersects the vertex.

Figure 1: Irregular Cone. It is irregular because of the non-circular shape of the directrix and its angle.

A right circular cone is formed when the directrix is a circle and the altitude intersects the plane of the base in the center of the circle. This kind of cone is used to create conic sections.

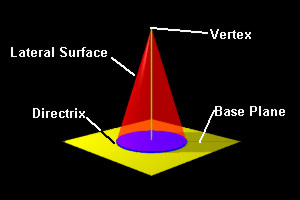Figure 2: A Right Cone

The Conic Sections:

A conic section is the shape formed on a plane passing through a right circular cone. The conic sections are the point, line, circle, ellipse, parabola, and hyperbola.

If the plane contains the vertex of the cone and does not intersect any other part of the cone, a point is formed on the plane.

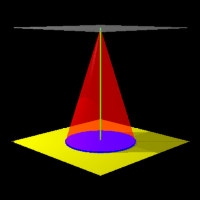Figure 3: A Point

If the plane contains the lateral surface of the cone, a line is formed on the plane.

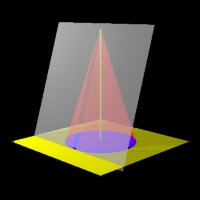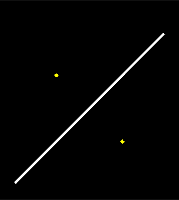Figure 4: A Line

If the plane is parallel to the base plane and does not contain the vertex, a circle is formed on the plane.

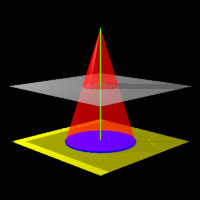Figure 5: A Circle

If the plane is tilted, but is not tilted enough to be parallel to the lateral surface and does not contain the vertex, an ellipse is formed on the plane.

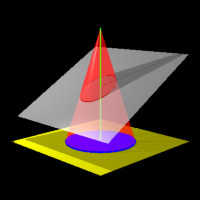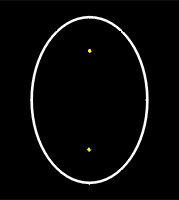Figure 6: An Ellipse

If the plane does not contain the vertex and is parallel to the lateral surface, a parabola is formed on the plane.

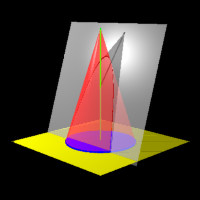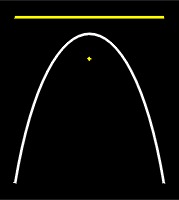Figure 7: A Parabola

If the plane is tilted at angle greater than that for a parabola and does not contain the vertex, a hyperbola is formed.

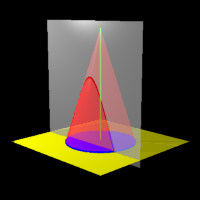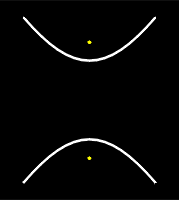Figure 8: A Hyperbola

The Point:

A point has no equation and is expressed by giving a value for every required axis. It is usually expressed as coordinates. In a two dimensional plane, a point has x and y coordinates. In a three dimensional coordinate system, a point has x, y, and z coordinates. These coordinates are written in parentheses. Example: (20, 38) for a point 20 units on the x axis and 38 units on the y axis.

The Line:

A line is defined as the locus of points equidistant to two fixed points.

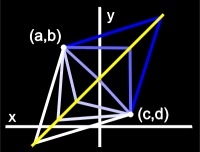Figure 9: The yellow line is equidistant from points (a,b) and (c,d)

The distance formula must be used twice when finding the equation of a line.

x and y are the x,y coordinates for any point on the line
a and b are the x,y coordinates for the first point
c and d are the x,y coordinates for the second point

The general way of writing a line is with a simpler equation. The following equation is in slope-intercept from.

x and y are the x,y coordinates for any point on the line
m is the slope of the line
b is the y intercept, the y coordinate for a point on the line when x = 0

The constant m is usually a fraction. If you pick two points on the line (c,d) and (e,f), you can then draw two lines from those points to point (e,d) to make a right triangle. The height of that triangle (f - d) will be the numerator of m and the width of the triangle (e - c) will be the denominator of m. B will be the value of y when x = 0, it is usually found after m is found. This triangle is illustrated in the following figure.

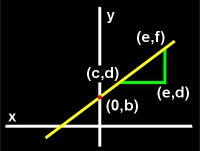Figure 10: Finding the value of m and b in the slope-intercept form of the equation of a line.

Finding the Distance from a Point to a Line

To find the distance from point 1 to line 1, the distance between point 1 and the closest point on line 1 to point 1 is found. The point on line 1 closest to point 1 is the point at the intersection of line 1 and a new line that is perpendicular to line 1 and that intersects point 1.

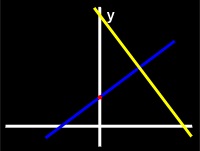Figure 11: The yellow line is the original line. The blue line is perpendicular to the yellow line and intersects the red point. The point at the intersection of the two lines is the closest point on the yellow line to the red point.

The slope of a line that is perpendicular to another line is the negative reciprocal of the first line's slope. The next two equations illustrate this.

The value for b is found for the equation of the new line that intersects point 1 by substituting the coordinates of point 1 in the equation for x and y and solving for b.

The equations of both lines are then combined using substitution after arranging each equation so that it equals 0. This will result in the coordinates of the point on line 1 that is closest to point 1 (the point at the intersection of the two lines).

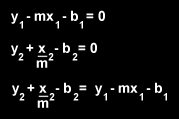
The distance formula is then used on these points and the distance from point 1 to line 1 is found.

The Circle:

A circle is defined as the locus of all points such that the distance from any one of these points to a fixed point is a constant.

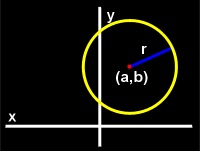Figure 12: A circle centered at point (a,b)

This means that for any point on the circle, the distance from the point to the center of the circle is the same as for any other point on the circle. This distance is the radius of the circle.

To find the equation of a circle, the distance formula must be used only once.

The equation of a circle follows.
x and y are the x,y coordinates for any point on the circle.
a and b are the x,y coordinates for the center of the circle.
r is the radius of the circle

The Ellipse:

The ellipse is defined as the locus of all points such that the sum of the distances from any one of these points to two fixed points (called foci) is a constant. This is shown in figure 12. The lengths of the lines D1 and D2 are the distances from a point on the ellipse to the foci.

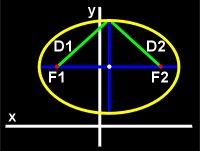Figure 12: An ellipse. The sum of D1 and D2 (the green lines) is always the same for any point on the ellipse.

An ellipse, unlike a circle, has two focus points. For each point on the ellipse, the sum of the distance (D1) from the point to the first focus (F1) and the distance (D2) from the point to the second focus (F2) is always a constant.

Every ellipse is symmetrical about two axes, the major and minor axes. The line segment that intersects both foci is called the major axis (shown above as the horizontal blue line). Half of the major axis is called the semimajor axis. The line perpendicular to the major axis is the minor axis (shown above as the vertical blue line).

The distance from the center of the ellipse to each of the two foci is always the same.

The major axis bisects and is bisected by the minor axis.

The major axis is perpendicular to the minor axis.

The center of the ellipse is always at the intersection of the two axes.

The sum of the lengths of the lines D1 and D2 (shown in figures 12 and 13 ) is always equal to the length of the major axis.

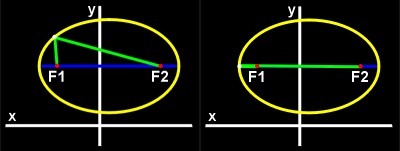Figure 13: An illustration of why the sum of the two green lines (D1 and D2) equals the length of the major axis. In the right ellipse, the distance from the point to F1 is covered twice. Thus, since the distance from the right side of the ellipse to F2 is equal to the distance from the left side of the ellipse to F1 (because the ellipse is symmetrical about its minor axis), and the distance from the left side to F2 is covered by D2, D1 can be moved to the right side of the ellipse, completing the length of the major axis.

Since the semimajor axis is half of the major axis, and since the sum of D1 and D2 equals the length of the major axis, then when the lines D1 and D2 are the same length (as they are shown in figure 14) then each one is also the same length as the semimajor axis.

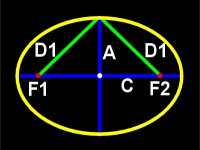Figure 14: A is half of the length of the minor axis. C is the distance from the center of the ellipse to F1 or F2.

By using the Pythagorean theorem, the lengths and orientations of the axes can be found if the positions of the two foci are known.

To find the equation of an ellipse, the distance formula must be used twice.

The equation of an ellipse follows.
x and y are the x,y coordinates for any point on the ellipse.
a and b are the x,y coordinates for the first focus
c and d are the x,y coordinates for the second focus
m is the sum of the two lengths

The Parabola and Hyperbola:

The parabola is important because its shape directs light to a central focal point. The mirrors of almost all modern reflecting telescopes are parabolic.

A parabola is the locus of all points that are equidistant from a line called the directrix and a point called the focus. This is illustrated in the following image.

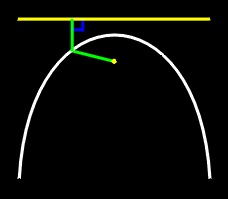Figure 15: A parabola

The Hyperbola will not be used extensively in this site but the definition is given here.

A hyperbola is the locus of all points such that the absolute value of the difference of the distances from one of these points to the two foci is a constant.

The equations for these can be found in most advanced math text books.

If you do not see frames, click here to go to the frames page.
If you do not want to use frames, click here to go to the non-frames home page and sitemap.